Unsigned와 Signed의 차이점
Unsigned : 부호가 없는 수 ( 양수와 음수의 구분이 없다.)
Signed: 부호가 있는 수 ( 양수와 음수를 구분한다.)
Unsigned는 부호가 없는 수로 1101 0011인 경우 10진수로 211을 의미한다.
직관적으로 8비트가 있는 경우, Unsigned는 0부터 255까지의 수의 표현이 가능하다.
Signed는 양수의 경우 Unsigned와 똑같다. 하지만 음수의 경우 여러가지 표현 법이 존재하는데, 표현법 모두 맨앞비트는 부호비트로 활용하여 실제 데이터를 표현할 수 있는 비트는 7비트로 부호비트표현 방법과 1의 보수 체계 방법의 경우 -127 ~ +127까지 표현 가능하고, 2의 보수 체계 방법일 때 8비트는 -128 ~ +127까지 표현이 가능하다.
signed의 음수 표현 방법에는 부호 비트 (Sign-magnitude representation), 1의 보수 (Ones' complement representation), 2의 보수 (Two's complement representation) 와 같이 3가지의 표현 방법이 존재한다.
부호 비트 (Sign-magnitude representation)

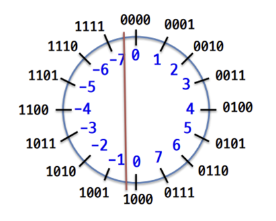
첫번쨰로 부호 비트 (Sign-magnitude representation) 표현 방법은 부호비트와 표현비트가 분리되어있다. 맨 앞 비트가 양수인지 음수인지 표현하는 비트로, b(w-2)비트가 1인 경우 음수이고 b(w-2)비트비트가 0인경우 양수이다.
부호비트 표현방법 특징으로 4비트를 표현한 예시를 보면 0을 표현하는 경우가 2가지가 존재한다.
맨앞 비트가 양수인지 음인지를 표현하기 떄문에, 1000과 0000 이 +0과 -0을 의미하여 0을 2가지로 표현이 가능하다.
이와 같은 부호비트표현 방법은 부동소수점 방식에 사용된다.
1의 보수 (Ones' complement representation)


두번째로 1의 보수 (Ones' complement representation)표현 방법이다. 부호비트표현방식과 같이 1의 보수의 경우에도 맨 앞비트를 부호비트로 활용한다.
1의 보수란 각 자리수의 값이 모두 1인 이진수에서 해당 이진수를 뺀 결과이다. 예시로 1010이란 이진수의 1의 보수는 0101이다. 쉽게 기억하기위해서는 이진수의 각자리수의 값을 0이면 1로 1이면 0으로 반전시킨다고 기억하면 쉽다.
이처럼 1의 보수로 음수를 표현 할 때, 4비트 예시를 보면 부호비트 표현방식과 똑같이 0이 2개인 것을 알 수있다.
현재 사용되지 않는 음수 표현 방식이다.
2의 보수 (Two's complement representation)


세번째로 2의 보수 (Two's complement representation)표현방법은 1의 보수+1의 형태이다. 앞선 방법들과 동일하게 맨 앞 비트는 부호비트로 활용한다.
2의 보수는 1의 보수에 +1을하여 표현하기 때문에 4비트 예시를 보면 0이 1개인것을 확인할 수 있다.
그러므로 부호비트방법과 1의 보수와 같이 4비트로 표현할수 있는 수의 범위가 -7~+7이 아닌 -8~+7로 1개의 수를 더 표현 할 수 있다.
하드웨어가 읽기 용이하여 최근에는 대부분이 2의 보수 체계를 채택하여 사용중이다.
'Computer Science' 카테고리의 다른 글
| [데이터 통신] 정보의 압축 ( 무 손실 압축, 손실 압축) (0) | 2024.04.14 |
|---|---|
| [컴퓨터 구조] 파이프라이닝과 해저드 ( Pipelining & Hazards) (1) | 2024.03.19 |
| [데이터 통신] 정보의 형태와 디지털화 ( 아날로그, 디지털 ) (2) | 2024.03.12 |
| [시스템 소프트웨어] 왜 컴퓨터에서는 10진수가 아닌 2진수를 사용할까? (1) | 2023.10.18 |
