문제
5972번: 택배 배송
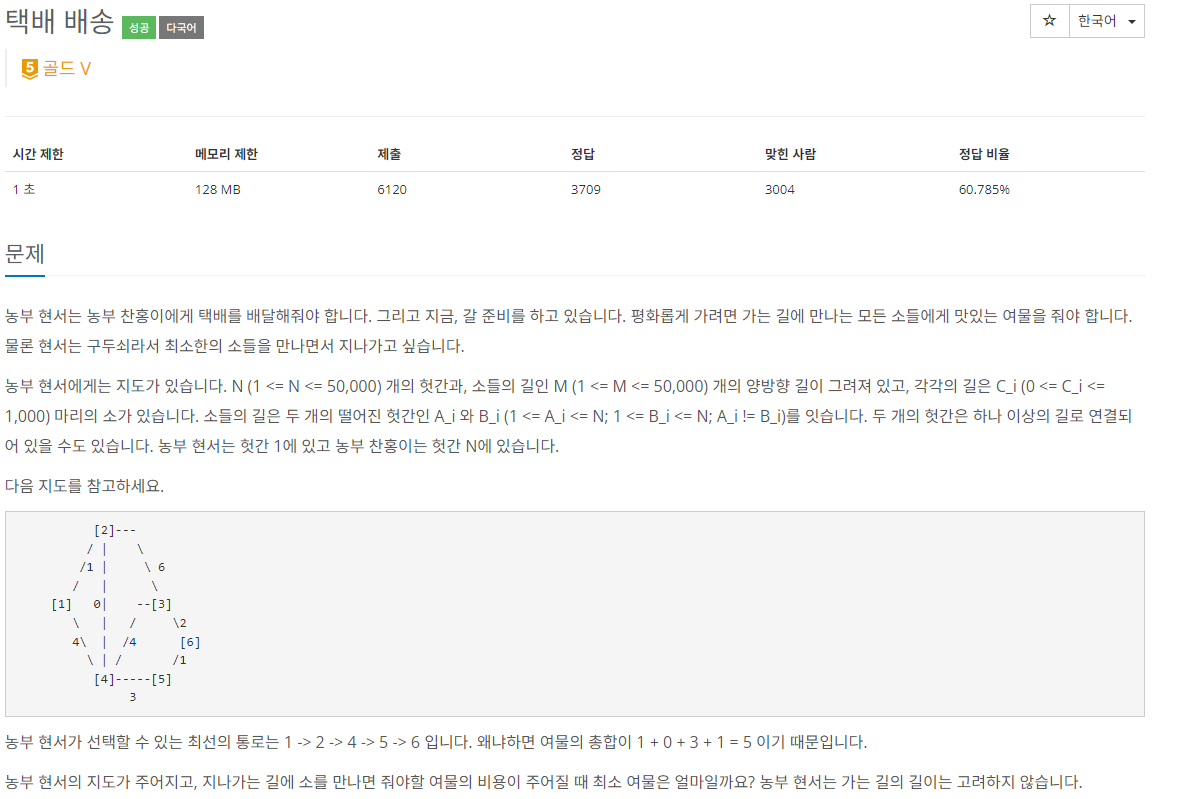
농부 현서는 농부 찬홍이에게 택배를 배달해줘야 합니다. 그리고 지금, 갈 준비를 하고 있습니다. 평화롭게 가려면 가는 길에 만나는 모든 소들에게 맛있는 여물을 줘야 합니다. 물론 현서는
www.acmicpc.net
정답 소스코드 (Python)
import heapq
v,e=map(int,input().split())
graph=[[]for _ in range(v+1)]
dis=[1e9]*(v+1)
for i in range(e):
v1,v2,e=map(int,input().split())
graph[v1].append([v2,e])
graph[v2].append([v1,e])
def dijkstra(start):
q=[]
heapq.heappush(q,(0,start))
dis[start]=0
while q:
distance,node=heapq.heappop(q)
if distance>dis[node]:continue
for next in graph[node]:
new_cost=next[1]+dis[node]
if new_cost<dis[next[0]]:
dis[next[0]]=new_cost
heapq.heappush(q,(new_cost,next[0]))
dijkstra(1)
print(dis[v])
풀이 (Python)
전형적인 최단거리를 묻는 문제이다. 다익스트라 알고리즘의 기본 활용 문제로써 풀이가 가능하다.
Point 1) 그래프 입력받기
v,e=map(int,input().split())
graph=[[]for _ in range(v+1)]
dis=[1e9]*(v+1)
for i in range(e):
v1,v2,e=map(int,input().split())
graph[v1].append([v2,e])
graph[v2].append([v1,e])graph를 구현하기 위해 빈 정점들을 선언해 준 후, 간선들을 이어준다. 무방향 그래프이기 때문에 양쪽 방향으로 다 이어주었다. dis는 각 정점의 최소 비용을 저장하는 리스트로서dis [12]인 경우 시작 지점부터 12 정점까지의 최소 비용을 저장하고 있다.
Point 2) 다익스트라 알고리즘 로직
def dijkstra(start):
q=[]
heapq.heappush(q,(0,start))
dis[start]=0
while q:
distance,node=heapq.heappop(q)
if distance>dis[node]:continue
for next in graph[node]:
new_cost=next[1]+dis[node]
if new_cost<dis[next[0]]:
dis[next[0]]=new_cost
heapq.heappush(q,(new_cost,next[0]))
파이썬 heapq라이브러리를 활용하여, BFS알고리즘과 비슷하게 사용한다.
최소비용의 간선을 선택하는 방식이기 때문에 heapq을 사용해야 한다.
while문은 q가 비어있을 때까지 진행되며, dis는 1e9=10^9으로 초기화되어 있기에 dis [node]보다 heap에서 pop 한 간선의 비용이 더 높은 경우 continue 한다. 초기화 이외에도 더 큰값은 비교할 이유가 없기에 바로 다음으로 continue한다.
각 정점에서 갈 수 있는 정점은 (현재 정점까지의 최소비용+간선 비용) < (해당 정점까지의 최소비용)을 만족한다면, 더 작은 값을 해당 정점의 최소비용으로 갱신 후 해당 정점으로 이동한다.
- 기본 로직
1. 정점을 방문 가능하면 heapq에 넣는다.
2. 해당 정점에 온 경우 heapq에서 pop 하여 연결 노드와 비용을 조건과 계산하여 다음 가능한 정점을 찾는다.
'Baekjoon' 카테고리의 다른 글
| [백준] 2668번 숫자고르기 (파이썬) (0) | 2024.02.06 |
|---|---|
| [백준] 9935번 문자열 폭발 (파이썬) (1) | 2024.02.05 |
| [백준] 1446번 지름길 (파이썬) (1) | 2024.01.28 |
| [백준] 2631번 줄 세우기 (파이썬) (1) | 2024.01.28 |
| [백준] 2503번 숫자 야구 (파이썬) (1) | 2024.01.28 |
